16. Ejercicios de programación PR03, PR04 y PR05

En esta página web te explican cuáles debieran ser los pasos para realizar un programa, no sólo en PYTHON, sino en cualquier lenguaje. Seguir sus instrucciones siempre será una forma de realizar el trabajo eficaz y profesionalmente. Leer el apartado 2.1 y 2.2.

Enlace: ¿cómo se debe programar?

PR03: Calcula la suma de los números naturales y el factorial (50 puntos)

La definición de factorial de un número natural es la del producto de todos los números naturales anteriores a él, desde el 1 al mismo. Así, el factorial del 5, 5! = 1 x 2 x 3 x 4 x 5

Más formalmente, se usa la fórmula n!=∏nk=1k

El programa que tienes que hacer debe calcular el factorial de un número, no permitir que sea un número menor que 1 y mayor que 100  (rechazar del 0 a los números negativos, y a partir del ciento uno). y de paso, calcular además del factorial la suma de la sucesión de números y la división del factorial entre la suma.

sum=∑nk=1k=1+...+n

n!sum

PR04: Calcula el producto escalar y vectorial de dos vectores (100 puntos)

El producto escalar

Tomando como base canónica R3, el producto escalar de dos vectores u=uxi+uyj+uzk  y  v=vxi+vyj+vzk sería:

u⋅v=(uxi+uyj+uzk)⋅(vxi+vyj+vzk)=ux⋅vx+uy⋅vy+uz⋅vz

El producto escalar también puede calcularse como:

u⋅v=|u |⋅|v |⋅cos(uvˆ)

El producto vectorial

El producto vectorial de dos vectores u y v, que pertenecen al espacio tridimensional,  es una aplicación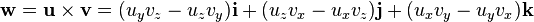
x:R3×R3→R3

(u,v)→u×v

En el que si u=uxi+uyj+uzk y v=vxi+vyj+vzk, entonces

Que se puede expresar como un determinante simbólico de orden 3, en el que la primera fija son los vectores unitarios en cada eje

u×v=∣∣∣∣iuxvxjuyvykuzvz∣∣∣∣=∣∣∣uyvyuzvz ∣∣∣⋅i−∣∣∣uxvxuzvz ∣∣∣⋅j+∣∣∣uxvxuyvy ∣∣∣⋅k

El producto vectorial pues es una iteración de tres bucles. El primer bucle recorre el vector simbólico (i,j,k) , el segundo los valores del vector u y el tercero el del vector v. Por cada valor del primer bucle, se deben multiplicar coordenadas del segundo y el tercero, y sus productos sumarse o restarse. Las coordenadas en la misma posición, o con el mismo índice que en el primer bucle, se desechan (o se hacen cero). En cada caso, hay que determinar el signo de cada multiplicación.

El módulo del producto escalar también puede calcularse como:

|w|=|u×v|=|u|⋅|v|⋅sin(uvˆ)

Explicación algoritmo producto vectorial

 

PR05: Calcula la ecuación de un plano en forma normal, dados dos vectores directores y un punto (EXTRA: 40 puntos)

Aquí tienes una explicación matemática:

El programa debe ser capaz de:

1. Pedir los datos de los dos vectores directores (funciones, iteración). Calcular sus módulos.
2. Pedir los datos del punto al que pertenece el plano.
3. Calcular el vector normal unitario (módulo 1) al plano. Basarse en programas anteriores.
4. Calcular la ecuación normal del plano.
5. Opcional: presentación de la ecuación elegante (el factor 0 implica que no aparece la incógnita, al principio de la ecuación no aparece el signo más, el factor 1 no aparece...) O sea, que aparezca por ejemplo:   x- 4.000 =0 , no +1.00x+0.00*y+0.00*z-4.000 = 0